数据结构实战

        B-树是一种平衡的多路查找树，它的结构和特性如下：

        一棵m阶的B-树，或为空树，或为满足下列特性的m叉树：

1. 树中每个结点至多有m棵子树；
2. 若根结点不是叶子结点，则至少有两棵子树；
3. 除根之外的所有非终端结点至少有棵子树；
4. 所有非终端结点中包含的信息数据为（n, A0, K1, A1, K2, A2, ..., Kn, An）；
5. 所有的叶子结点都出现在同一层次上，并且不带信息。

        下面我们就来实现一个3阶的B-树。对于B-树的查找、插入、删除不作过多的说明，只用代码实现其功能。

        首先定义B-树的数据结构：

typedef union
{
	int key;
	struct s_node *child;
} s_point_key;

typedef struct s_pk_node
{
	struct s_node *header;
	s_point_key *pk;
	struct s_pk_node *pre;
	struct s_pk_node *next;
} s_pk_node;

typedef struct s_node
{
	s_pk_node *parent;
	int key_num;
	s_pk_node *pk_node;
} s_node;

typedef struct s_tree
{
	//根节点
	s_node *root;
	//阶
	int m;
} s_tree;

        实现查找算法：

s_node* tree_search(s_node *node, int key)
{
	if (node == null)
	{
		return null;
	}

	s_pk_node *p = node->pk_node;

	for (int i = 0; i < 2 * node->key_num + 1 && p != null; i++)
	{
		//key
		if (i % 2 == 1)
		{

			if (key == p->pk->key)
			{
				return p->header;
			}
			// <
			else if (key < p->pk->key)
			{
				if (p->pre->pk->child == null)
				{
					return null;
				}
				else
				{
					return tree_search(p->pre->pk->child, key);
				}
			}
			// >
			else
			{
				if ((p->next->next != null && key < p->next->next->pk->key) || (p->next->next == null && p->next->pk->child != null))
				{
					return tree_search(p->next->pk->child, key);
				}
			}

		}
		p = p->next;
	}

	return null;
}

        实现插入新关键字结点，插入是如果结点中关键字数大于m-1则做结点分裂操作：

bool tree_insert_node(s_tree *tree, s_pk_node *pk_node, s_node *node, int key)
{
	if (tree == null)
	{
		return false;
	}

	if (node == null)
	{
		node = (s_node *) malloc(sizeof(s_node));
		node->parent = pk_node;
		node->key_num = 0;
		node->pk_node = null;

		if (pk_node != null)
		{
			pk_node->pk->child = node;
		}

		if (tree->root == null)
		{
			tree->root = node;
		}
	}

	if (node->key_num == 0)
	{
		s_point_key *pk_pre = (s_point_key *) malloc(sizeof(s_point_key));
		pk_pre->child = null;

		s_point_key *pk_key = (s_point_key *) malloc(sizeof(s_point_key));
		pk_key->key = key;

		s_point_key *pk_next = (s_point_key *) malloc(sizeof(s_point_key));
		pk_next->child = null;

		s_pk_node *pk_node_pre = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_pre->header = node;
		pk_node_pre->pk = pk_pre;

		s_pk_node *pk_node_key = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_key->header = node;
		pk_node_key->pk = pk_key;

		s_pk_node *pk_node_next = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_next->header = node;
		pk_node_next->pk = pk_next;

		pk_node_pre->pre = null;
		pk_node_pre->next = pk_node_key;

		pk_node_key->pre = pk_node_pre;
		pk_node_key->next = pk_node_next;

		pk_node_next->pre = pk_node_key;
		pk_node_next->next = null;

		node->pk_node = pk_node_pre;

		node->key_num++;

		return true;
	}

	s_pk_node *p = node->pk_node;

	for (int i = 0; i < 2 * node->key_num + 1 && p != null; i++)
	{
		//key
		if (i % 2 == 1)
		{

			if (key == p->pk->key)
			{
				return true;
			}
			// <
			else if (key < p->pk->key)
			{
				if (p->pre->pk->child == null)
				{
					tree_insert_pk_node(p, 0, key);
					node->key_num++;
					tree_split_node(tree, node);

					return true;
				}
				else
				{
					return tree_insert_node(tree, p->pre, p->pre->pk->child, key);
				}
			}
			// >
			else
			{
				if ((p->next->next != null && key < p->next->next->pk->key && p->next->pk->child == null) || (p->next->next == null && p->next->pk->child == null))
				{
					tree_insert_pk_node(p, 1, key);
					node->key_num++;
					tree_split_node(tree, node);

					return true;
				}
				else if (p->next->next != null && key < p->next->next->pk->key && p->next->pk->child != null)
				{
					return tree_insert_node(tree, p->next, p->next->pk->child, key);
				}
				else if (p->next->next == null && p->next->pk->child != null)
				{
					return tree_insert_node(tree, p->next, p->next->pk->child, key);
				}
			}

		}
		p = p->next;
	}

	return true;
}

void tree_insert_pk_node(s_pk_node *pk_node, int type, int key)
{
	if (type == 0)
	{
		s_point_key *pk_key = (s_point_key *) malloc(sizeof(s_point_key));
		pk_key->key = key;

		s_point_key *pk_pre = (s_point_key *) malloc(sizeof(s_point_key));
		pk_pre->child = null;

		s_pk_node *pk_node_key = (s_pk_node *) malloc(sizeof(s_pk_node));
		s_pk_node *pk_node_pre = (s_pk_node *) malloc(sizeof(s_pk_node));

		pk_node_key->header = pk_node->header;
		pk_node_key->pk = pk_key;
		pk_node_pre->header = pk_node->header;
		pk_node_pre->pk = pk_pre;

		pk_node_pre->pre = pk_node->pre->pre;
		pk_node->pre->pre = pk_node_key;
		pk_node_key->next = pk_node->pre;
		pk_node_key->pre = pk_node_pre;
		pk_node_pre->next = pk_node_key;
		if (pk_node_pre->pre != null)
		{
			pk_node_pre->pre->next = pk_node_pre;
		}
		else
		{
			pk_node->header->pk_node = pk_node_pre;
		}
		pk_node_pre->header = pk_node->header;
		pk_node_key->header = pk_node->header;
	}
	//next
	else if (type == 1)
	{
		s_point_key *pk_key = (s_point_key *) malloc(sizeof(s_point_key));
		pk_key->key = key;

		s_point_key *pk_next = (s_point_key *) malloc(sizeof(s_point_key));
		pk_next->child = null;

		s_pk_node *pk_node_key = (s_pk_node *) malloc(sizeof(s_pk_node));
		s_pk_node *pk_node_next = (s_pk_node *) malloc(sizeof(s_pk_node));

		pk_node_key->header = pk_node->header;
		pk_node_key->pk = pk_key;
		pk_node_next->header = pk_node->header;
		pk_node_next->pk = pk_next;

		pk_node_next->next = pk_node->next->next;
		pk_node->next->next = pk_node_key;
		pk_node_key->pre = pk_node->next;
		pk_node_key->next = pk_node_next;
		pk_node_next->pre = pk_node_key;
		if (pk_node_next->next != null)
		{
			pk_node_next->next->pre = pk_node_next;
		}

		pk_node_key->header = pk_node->header;
		pk_node_next->header = pk_node->header;
	}
}

void tree_split_node(s_tree *tree, s_node *node)
{
	if (node->key_num < tree->m)
	{
		return;
	}

	s_pk_node *pk_parent = node->parent;

	int m = node->key_num;

	int p_num = divup(m, 2) - 1;
	s_node *p = (s_node *) malloc(sizeof(s_node));
	p->key_num = p_num;
	p->parent = pk_parent;
	p->pk_node = node->pk_node;

	s_pk_node *p_pk = node->pk_node;
	for (int i = 0; i < p_num; i++)
	{
		//pointer
		p_pk->header = p;
		p_pk = p_pk->next;
		//key
		p_pk->header = p;
		p_pk = p_pk->next;
	}

	s_pk_node *r = p_pk->next;

	p_pk->header = p;
	p_pk->next->pre = null;
	p_pk->next = null;

	s_node *q = node;
	int q_num = m - divup(m, 2);
	q->parent = pk_parent;
	q->key_num = q_num;
	q->pk_node = r->next;
	q->pk_node->pre = null;

	s_pk_node *q_pk = node->pk_node;
	for (int i = 0; i < q_num; i++)
	{
		//pointer
		q_pk->header = q;
		q_pk = q_pk->next;
		//key
		q_pk->header = q;
		q_pk = q_pk->next;
	}

	if (q_pk != null)
	{
		q_pk->header = q;
	}

	r->pre = null;
	r->next = null;

	if (pk_parent == null)
	{
		s_node *p_new = (s_node *) malloc(sizeof(s_node));
		p_new->parent = null;
		p_new->key_num = 0;
		p_new->pk_node = null;

		tree->root = p_new;

		s_point_key *pk_pre = (s_point_key *) malloc(sizeof(s_point_key));
		pk_pre->child = p;

		s_point_key *pk_next = (s_point_key *) malloc(sizeof(s_point_key));
		pk_next->child = q;

		s_pk_node *pk_node_pre = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_pre->header = p_new;
		pk_node_pre->pk = pk_pre;

		s_pk_node *pk_node_next = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_next->header = p_new;
		pk_node_next->pk = pk_next;

		pk_node_pre->pre = null;
		pk_node_pre->next = r;

		r->pre = pk_node_pre;
		r->next = pk_node_next;
		r->header = p_new;

		pk_node_next->pre = r;
		pk_node_next->next = null;

		p->parent = pk_node_pre;
		q->parent = pk_node_next;

		p_new->pk_node = pk_node_pre;
		p_new->key_num++;

		node = p_new;
	}
	else
	{
		s_point_key *pk_next = (s_point_key *) malloc(sizeof(s_point_key));
		s_pk_node *pk_node_next = (s_pk_node *) malloc(sizeof(s_pk_node));
		pk_node_next->pk = pk_next;

		r->next = pk_node_next;
		pk_node_next->pre = r;
		pk_node_next->next = pk_parent->next;
		pk_node_next->header = pk_parent->header;

		if (pk_parent->next != null)
		{
			pk_parent->next->pre = pk_node_next;
		}

		pk_parent->pk->child = p;
		pk_parent->next = r;
		r->pre = pk_parent;
		r->header = pk_parent->header;

		q->parent = pk_node_next;
		pk_node_next->pk->child = q;

		pk_parent->header->key_num++;

		node = pk_parent->header;
	}

	tree_split_node(tree, node);
}

        实现删除功能，对于特殊情况做结点合并操作：

bool tree_del_node(s_tree *tree, s_node *node, int key)
{
	if (tree == null)
	{
		return false;
	}

	if (node == null)
	{
		return false;
	}

	s_node *p_del = tree_search(node, key);
	if (p_del == null)
	{
		return false;
	}

	s_pk_node *pk_node_del = tree_find_pk_node(p_del, key);
	if (pk_node_del == null)
	{
		return false;
	}

	if (!tree_is_leaf(p_del))
	{
		s_pk_node *pk_node_min = null;
		if (pk_node_del->next->pk->child == null)
		{
			pk_node_min = pk_node_del->next->next;
		}
		else
		{
			pk_node_min = tree_min_key(pk_node_del->next->pk->child);
		}

		if (pk_node_min == null)
		{
			return false;
		}

		pk_node_del->pk->key = pk_node_min->pk->key;

		tree_del_node(tree, pk_node_min->header, pk_node_min->pk->key);
	}

	int num = divup(tree->m, 2);
	if (p_del->key_num >= num)
	{
		s_pk_node *pre = pk_node_del->pre;
		pre->next = pk_node_del->next->next;
		if (pre->next != null)
		{
			pre->next->pre = pre;
		}
		free(pk_node_del);
		p_del->key_num--;
		return true;
	}

	if (p_del->key_num == num - 1)
	{
		if (p_del->parent == null)
		{
			s_pk_node *pk = p_del->pk_node;
			while (pk->next != null)
			{
				if (pk->next == pk_node_del)
				{
					pk->next = pk_node_del->next->next;
					if (pk_node_del->next->next != null)
					{
						pk_node_del->next->next->pre = pk;
					}
					free(pk_node_del);
				}
				pk = pk->next;
			}
			p_del->key_num--;
			if (p_del->key_num == 0)
			{
				tree->root = null;
				free(p_del);
			}
			return true;
		}

		if (p_del->parent->next != null && p_del->parent->next->next->pk->child != null)
		{
			if (p_del->parent->next->next->pk->child->key_num > num - 1)
			{
				s_pk_node *pkn = p_del->parent->next->next->pk->child->pk_node;
				pk_node_del->pk->key = p_del->parent->next->pk->key;
				p_del->parent->next->pk->key = p_del->parent->next->next->pk->child->pk_node->next->pk->key;
				p_del->parent->next->next->pk->child->pk_node = p_del->parent->next->next->pk->child->pk_node->next->next;
				p_del->parent->next->next->pk->child->pk_node->next->next->pre = null;
				p_del->parent->next->next->pk->child->key_num--;

				free(pkn->next);
				free(pkn);

				return true;
			}
			else if (p_del->parent->next->next->pk->child->key_num == num - 1)
			{
				tree_merge(tree, p_del, pk_node_del);
				return true;
			}
		}

		if (p_del->parent->pre != null && p_del->parent->pre->pre->pk->child != null)
		{
			if (p_del->parent->pre->pre->pk->child->key_num > num - 1)
			{
				pk_node_del->pk->key = p_del->parent->pre->pk->key;

				s_pk_node *pk_max = p_del->parent->pre->pre->pk->child->pk_node;
				while (pk_max->next != null)
				{
					pk_max = pk_max->next;
				}
				pk_max = pk_max->pre;

				p_del->parent->pre->pk->key = pk_max->pk->key;
				pk_max->pre->next = null;
				p_del->parent->pre->pre->pk->child->key_num--;

				free(pk_max->next);
				free(pk_max);

				return true;
			}
			else if (p_del->parent->pre->pre->pk->child->key_num == num - 1)
			{
				tree_merge(tree, p_del, pk_node_del);
				return true;
			}
		}
		return false;
	}
	return false;
}

void tree_merge(s_tree *tree, s_node *p_del, s_pk_node *pk_node_del)
{
	int num = divup(tree->m, 2);

	if (p_del->parent->next != null && p_del->parent->next->next->pk->child != null)
	{
		if (p_del->parent->next->next->pk->child->key_num == num - 1)
		{
			s_node *right_node = p_del->parent->next->next->pk->child;
			s_pk_node *p = p_del->pk_node;
			int tnum = p_del->key_num;
			s_pk_node *parent_p = p_del->parent;
			s_pk_node *parent_key = parent_p->next;
			s_pk_node *parent_n = parent_key->next;
			for (int i = 0; i < 2 * p_del->key_num + 1; i++)
			{
				if (i % 2 == 1)
				{
					if (p == pk_node_del)
					{
						p = p->pre;
						p->next = pk_node_del->next->next;
						if (pk_node_del->next->next != null)
						{
							pk_node_del->next->next->pre = p;
						}
						p = p_del->pk_node;
						pk_node_del->pk->key = parent_key->pk->key;
						while (p->next != null)
						{
							p = p->next;
						}
						p->next = pk_node_del;
						pk_node_del->pre = p;

						p = p_del->pk_node;
						s_node *right_node = parent_n->pk->child;
						right_node->pk_node->next->pre = pk_node_del->next;
						pk_node_del->next->next = right_node->pk_node->next;
						right_node->pk_node->next = p;
						p->pre = right_node->pk_node;
						right_node->key_num += tnum;

						free(p_del);
					}
				}
				p = p->next;
			}

			return;
		}
	}
}

        编写一个main函数来测试这个B-树：

int main(int argc, char **args)
{

	//初始化3阶B-树
	s_tree tree;
	tree_init(&tree, 3);

	tree_insert(&tree, 1);
	tree_insert(&tree, 3);
	tree_insert(&tree, 2);
	tree_insert(&tree, 4);
	tree_insert(&tree, 6);
	tree_insert(&tree, 7);
	tree_insert(&tree, 9);
	tree_insert(&tree, 8);
	tree_insert(&tree, 0);
	tree_insert(&tree, 5);

	tree_del(&tree, 3);

	for (int i = 0; i < 10; ++i)
	{
		s_node *p = tree_search(tree.root, i);
		if (p == null)
		{
			printf("NG %d.\n", i);
		}
		else
		{
			printf("OK %d.\n", i);
		}
	}
	//销毁树
	tree_destroy(&tree);

	return 0;
}

        运行结果：

OK 0.
OK 1.
OK 2.
NG 3.
OK 4.
OK 5.
OK 6.
OK 7.
OK 8.
OK 9.

        我们来看这下这棵数的结构：

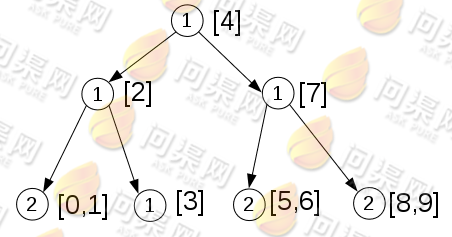
        本例代码：

code path   chapter.07/e.g.7.5/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure