数据结构实战

        广度优先的原则是从图的一个顶点出发，依次访问它的相邻节点，接着从这些相邻节点出发再访问它们的相邻节点。并使“先被访问的顶点的相邻节点”先于“后被访问的顶点的相邻节点”被访问。直到图中所有的顶点均被访问。例如下图：

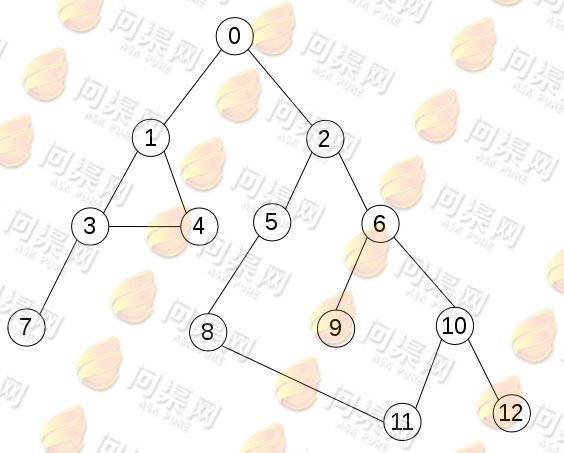
        上图的广度优先访问顺序为：

0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 12

        来看一下程序的实现过程。这里需要引入一个辅助的数据结构——队列。用队列来存放当前顶点的相邻节点。

//广度优先搜索
bool graph_breadth_first_search(s_graph *graph)
{
	if (graph == null)
	{
		return false;
	}

	//设置队列
	s_queue queue;
	init_queue(&queue, sizeof(int), free_int, null);

	//设置顶点已访问标志
	bool visited[graph->size];
	for (int i = 0; i < graph->size; i++)
	{
		visited[i] = false;
	}

	//访问所有的顶点
	for (int i = 0; i < graph->size; i++)
	{
		//深度广先访问顶点
		graph_bfs(graph, i, visited, &queue);
	}

	//销毁队列
	destroy_queue(&queue);

	return true;
}

//广度优先访问顶点递归算法
void graph_bfs(s_graph *graph, int v_ind, bool *visited, s_queue *queue)
{
	//如果此顶点已被访问，则直接返回
	if (visited[v_ind])
	{
		return;
	}

	//设置此顶点为已访问
	visited[v_ind] = true;

	//调用访问回调函数访问此节点
	graph->visit_vertex(graph->vertex[v_ind]);

	//取得下一条边
	s_arccell *ac = graph->vertex[v_ind].arccel_first;
	//循环所有关联i的边
	while (ac != null)
	{
		//将此顶点的关联顶点加入队列
		int *ival = malloc(sizeof(int));
		*ival = ac->i_index;
		queue_in(queue, ival);

		//如果还有下一条j相关的边
		s_arccell *ac_p = graph->vertex[ac->j_index].arccel_first;
		while (ac_p != null)
		{
			//将此顶点的关联顶点加入队列
			int *jval = malloc(sizeof(int));
			*jval = ac_p->j_index;
			queue_in(queue, jval);

			ac_p = ac_p->next_j;
		}

		//下一条i边
		ac = ac->next_i;
	}

	//如果队列不为空，即：出队列成功
	int *vertex = null;
	if (queue_out(queue, (void**) &vertex))
	{
		//对此顶点进行广度优先搜索
		graph_bfs(graph, *vertex, visited, queue);
	}
}

        再来看一下main函数：

#include <stdio.h>
#include <stdlib.h>
#include "graph.h"

int main(int argc, char **args)
{
	//邻接表
	s_graph graph;
	graph_init(&graph, 13, &visit_int, &visit_int);

    /*
     * 初始化数据部分代码略
     */

	//深度优先遍历图
	graph_breadth_first_search(&graph);

	//销毁邻接表
	graph_destroy(&graph);

	return 0;
}

        运行结果：

0 1 2 3 4 5 6 7 8 9 10 11 12

        本例代码：

code path   chapter.06/e.g.6.6/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure