数据结构实战

          第二节 矩阵压缩与转置

 

 

一、矩阵的表示与压缩

        在数学中多维矩阵通常用数组来表示，这里我们只学习二维矩阵的相关知识，多维矩阵与二维矩阵本质上没有区别，只是在逻辑上比二维矩阵复杂。

        我们所说的二维矩阵（以下简称矩阵）通常是使用二维数组来表示，例如一个5×6的矩阵可以这样表示：

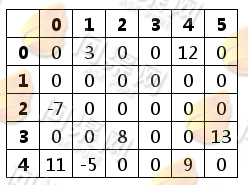
        对于矩阵中0值元素的数量很多时，可以使用3元组矩阵表示法。即：用（行号，列号，值）这3个数字为1组来表示一个元素的位置。那么上面的矩阵就可以表示为：

(0, 1, 3), (0, 4, 12), (2, 0, -7), (3, 2, 8), (3, 5, 13), (4, 0, 11), (4, 1, -5), (4, 4, 9)

        这样就起到了矩阵压缩的作用。

        我们首先定义一下3元组矩阵的数据结构：

//三元组
typedef struct
{
	//行号
	int i;
	//列号
	int j;
	//值
	int val;
} m_data;

//二维矩阵
typedef struct
{
	//总行数
	int m;
	//总列数
	int n;
	//非0元素个数
	int k;
	//线性三元组
	m_data *data;
} matrix;

        对矩阵使用3元组压缩算法如下：

//原始矩阵
int original_matrix[5][6] =
{
{ 0, 3, 0, 0, 12, 0 },
{ 0, 0, 0, 0, 0, 0 },
{ -7, 0, 0, 0, 0, 0 },
{ 0, 0, 8, 0, 0, 13 },
{ 11, -5, 0, 0, 9, 0 } };

//压缩矩阵
matrix mat;
mat.m = 5;
mat.n = 6;
mat.k = 0;
//8个非空元素
mat.data = (m_data *) malloc(sizeof(m_data) * 8);

//将原始矩阵压缩
for (int i = 0; i < mat.m; ++i)
{
	for (int j = 0; j < mat.n; ++j)
	{
		if (original_matrix[i][j] != 0)
		{
			/*
			 * 注意 mat.data + k的真正含义：
			 * 在指针data值（地址）上每加1,表示对这个地址加上一个单位的m_data（因为此指针是指向m_data类型）大小
			 * 因为 sizeof(m_data) == 12 == 0xc
			 * 假设：	mat.data 	 == 0x90cb008
			 * 			mat.data + 1 == 0x90cb014
			 * 			mat.data + 2 == 0x90cb020
			 * 			mat.data + 3 == 0x90cb02c
			 * 			mat.data + 4 == 0x90cb038
			 */
			set_data(mat.data + mat.k, i, j, original_matrix[i][j]);
			mat.k++;
		}
	}
}

//显示矩阵内容
//(0, 1, 3), (0, 4, 12), (2, 0, -7), (3, 2, 8), (3, 5, 13), (4, 0, 11), (4, 1, -5), (4, 4, 9)
for (int p = 0; p < mat.k; ++p)
{
	printf("(%d, %d, %d), ", mat.data[p].i, mat.data[p].j, mat.data[p].val);
}
printf("\n");

        运行结果：

(0, 1, 3), (0, 4, 12), (2, 0, -7), (3, 2, 8), (3, 5, 13), (4, 0, 11), (4, 1, -5), (4, 4, 9)

 

二、矩阵转置

        矩阵转置就是将矩阵元素的行号与列号互换：

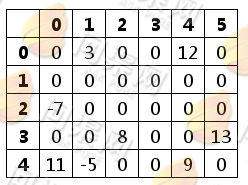
        转置后矩阵如下：

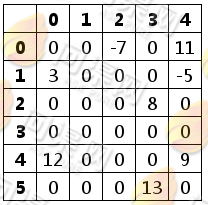
        我们首先实现矩阵的直接转置算法：

//转置矩阵
matrix r_mat;
r_mat.data = (m_data *) malloc(sizeof(m_data) * 8);
r_mat.m = mat.n;
r_mat.n = mat.m;
r_mat.k = mat.k;

int q = 0;
//从原始矩阵的每一列开始遍历，也就是转置矩阵中的行号
for (int col = 0; col < mat.n; ++col)
{
	//在mat中的所有3元组中查找
	for (int p = 0; p < mat.k; ++p)
	{
		//原矩阵中“列号”等于转置矩阵中行号
		if (mat.data[p].j == col)
		{
			//行列转置
			r_mat.data[q].i = mat.data[p].j;
			r_mat.data[q].j = mat.data[p].i;
			r_mat.data[q].val = mat.data[p].val;
			q++;
		}
	}
}

printf("\n");
for (int p = 0; p < r_mat.k; ++p)
{
	printf("(%d, %d, %d), ", r_mat.data[p].i, r_mat.data[p].j, r_mat.data[p].val);
}

        这种转置算法很好理解，就是在原矩阵的列中找到转置矩阵中的行。运行结果：

(0, 2, -7), (0, 4, 11), (1, 0, 3), (1, 4, -5), (2, 3, 8), (4, 0, 12), (4, 4, 9), (5, 3, 13)

        下面我们再来实现一种快速转置的算法：

//迅速转置矩阵
matrix e_mat;
e_mat.data = (m_data *) malloc(sizeof(m_data) * 8);
e_mat.m = mat.n;
e_mat.n = mat.m;
e_mat.k = mat.k;

//用于记录矩阵每一列中有多少个非0元素
int *num = (int *) malloc(sizeof(int) * mat.n);
//用于记录矩阵每一列第一个非0元素的开始位置（行号）
int *cpot = (int *) malloc(sizeof(int) * mat.n);

//初始化num，全部设为0
for (int j = 0; j < mat.n; ++j)
{
	num[j] = 0;
}
//计算矩阵每一列中有多少个非0元素
for (int q = 0; q < mat.k; ++q)
{
	++num[mat.data[q].j];
}
//初始号为0
cpot[0] = 0;
//计算每一列第一个非0元素的开始位置
for (int col = 1; col < mat.n; ++col)
{
	cpot[col] = cpot[col - 1] + num[col - 1];
}
//转置矩阵
int col;
for (int p = 0; p < mat.k; ++p)
{
	//取得列号
	col = mat.data[p].j;
	//从cpot中得到开始的位置
	q = cpot[col];
	//转置矩阵元素
	e_mat.data[q].i = mat.data[p].j;
	e_mat.data[q].j = mat.data[p].i;
	e_mat.data[q].val = mat.data[p].val;
	//此列的开始位置加一（转置矩阵的行号）
	++cpot[col];
}

printf("\n\n");
for (int p = 0; p < r_mat.k; ++p)
{
	printf("(%d, %d, %d), ", e_mat.data[p].i, e_mat.data[p].j, e_mat.data[p].val);
}

        可以看到这种快速转置算法是4个顺序执行的for循环语句，但在非0元素个数与m×n个数在同一个数量级时，快速转置算法会比原转置算法快的多。

        运行结果：

(0, 2, -7), (0, 4, 11), (1, 0, 3), (1, 4, -5), (2, 3, 8), (4, 0, 12), (4, 4, 9), (5, 3, 13)

       

        本例代码：

code path   chapter.04/e.g.4.2/

https       https://github.com/magicworldos/datastructure.git
git         git@github.com:magicworldos/datastructure.git
subverion   https://github.com/magicworldos/datastructure